Table of Contents
Sentence alignment algorithm
Definitions
Part 1
This part shows how sentences are represented.
- Let $L$ be a sequence of sentences with $l_1,\ldots,l_n$ being the concrete sentences.
| $L_1$ | $l_1$ | Frau Präsidentin! |
| $l_2$ | Meiner Auffassung nach ist es zu begrüßen, daß heute hier im Plenum ein so wichtiges Paket zur Volksgesundheit debattiert wird. | |
| $l_3$ | Vielleicht ist die Abendsitzung ein ungünstiger Zeitpunkt, da weniger Abgeordnete und andere mögliche Zuhörer anwesend sind, aber die Debatte ist dennoch wichtig. | |
| $l_4$ | Ich möchte die Schlußworte von Herrn Poggiolini aufgreifen und Herrn Viceconte zu seinem Bericht gratulieren. | |
| $l_5$ | Ich danke ihm auch dafür, daß er den Großteil der von den anderen Fraktionen eingereichten Änderungsanträge aufgenommen hat. | |
| $l_6$ | Mein Kollege Pedro Marset wird später einige der von uns in den Änderungsanträgen gemachten Vorschläge erläutern, die der Berichterstatter freundlicherweise aufgenommen hat. | |
| $l_7$ | In Anbetracht der Kürze der mir zur Verfügung stehenden Zeit habe ich den Ausführungen von Herrn Poggiolini zur Alzheimer-Krankheit kaum etwas hinzuzufügen. | |
| $L_2$ | $l_1$ | Madam President, I think we must welcome the fact that we are debating such an important set of public health matters today in this Chamber, although it is perhaps a pity that it is during the evening session when fewer Members take part and there is less chance of other people listening. |
| $l_2$ | Nevertheless, it is important. | |
| $l_3$ | Starting where Mr Poggiolini left off, I must congratulate Mr Viceconte on his report and thank him for including most of the amendments presented by the other groups. | |
| $l_4$ | Mr Marset Campos will speak later on and will have plenty to say about some of the proposals we made in the amendments which the rapporteur has very kindly accepted from us. | |
| $l_5$ | Anyway, in the short time allocated to me I do not want to say much more about Alzheimer’s disease than Mr Poggiolini has already said. | |
| $L_3$ | $l_1$ | Madame le Président, je pense qu’il faut saluer le fait que cette Assemblée débatte aujourd’hui aussi largement de la santé publique ; |
| $l_2$ | peut-être est-il dommage que ce débat ait lieu en séance nocturne, car la participation des députés et d’autres auditeurs est moindre, mais c’est important. | |
| $l_3$ | Je commencerai par où M Poggiolini a terminé ; | |
| $l_4$ | il faut féliciter M. Viceconte pour son rapport et le remercier d’avoir repris la majorité des amendements présentés par les autres groupes. | |
| $l_5$ | Mon collègue Pedro Marset interviendra plus tard et abondera dans certaines propositions que nous avons présentées dans les amendements que le rapporteur a très aimablement repris. | |
| $l_6$ | En tout cas, en si peu de temps, ne j’ai pas grand chose à ajouter à ce que M. Poggiolini a dit au sujet de la maladie d’Alzheimer. |
- Let $\mathcal{L}$ be a list of sentence sequences $L_1,\ldots,L_n$ with $L_j$ representing language $j$.
$\mathcal{L} = (L_1,L_2,L_3)$
Part 2
This part defines defines alignments as an ordered pair of position and alignment vectors.
- Let $\vec{p}_t$ be a position vector defining the position in $\mathbb{N}_0^{|\mathcal{L}|}$ where we want to depart from when searching for alignments at time $t$.
The position vector is defined a priori before the first and after the last alignment step: $\vec{p}_0 = \vec{0}$ and $\vec{p}_{t_{max}} = \begin{pmatrix} |L_1| \\ \vdots \\ |L_{|\mathcal{L}|}| \end{pmatrix}$.
$\vec{p}_0 = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}$, $\vec{p}_1 = \begin{pmatrix} 3 \\ 2 \\ 2 \end{pmatrix}$, $\vec{p}_2 = \begin{pmatrix} 5 \\ 3 \\ 4 \end{pmatrix}$, $\vec{p}_3 = \begin{pmatrix} 6 \\ 4 \\ 5 \end{pmatrix}$, $\vec{p}_4 = \begin{pmatrix} 7 \\ 5 \\ 6 \end{pmatrix}$
- Let $\vec{a}$ be an alignment vector defining how many sentences of each language are aligned to each other.
Three sentences of language $l_1$ are aligned with two sentences of $l_2$ and $l_3$:
$\vec{a} = \begin{pmatrix} 3 \\ 2 \\ 2 \end{pmatrix}$
- Let $A = (\vec{p},\vec{a})$ be an alignment constituted by a position vector $\vec{p}$ and an alignment vector $\vec{a}$.
$A_1 = (\vec{p}_1,\vec{a}_1) = \left(\begin{pmatrix} 3 \\ 2 \\ 2 \end{pmatrix},\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}\right)$
- Let $\Delta_r = \left( \vec{a}_1,\ldots,\vec{a}_{t_{max}} \right)$ be the sequence of alignment vectors $\vec{a}_i$ for run $r$ such that $\sum_{i=1}^{t_{max}}{a_i} = \begin{pmatrix} |L_1| \\ \vdots \\ |L_{|\mathcal{L}|}| \end{pmatrix}$.
$\Delta = \left( \begin{pmatrix} 3\\ 2\\ 2 \end{pmatrix},\begin{pmatrix} 2\\ 1\\ 2 \end{pmatrix},\begin{pmatrix} 1\\ 1\\ 1 \end{pmatrix},\begin{pmatrix} 1\\ 1\\ 1 \end{pmatrix} \right)$
That corresponds to the alignments
$\left( \begin{pmatrix} (l^1_1,\ldots,l^1_3)\\ (l^2_1,l^2_2)\\ (l^3_1,l^3_2) \end{pmatrix},\begin{pmatrix} (l^1_4,l^1_5)\\ (l^2_3)\\ (l^3_3,l^3_4) \end{pmatrix},\begin{pmatrix} (l^1_6)\\ (l^2_4)\\ (l^3_5) \end{pmatrix},\begin{pmatrix} (l^1_7)\\ (l^2_5)\\ (l^3_6) \end{pmatrix} \right)$
$\sum_{i=1}^4{a_i} = \begin{pmatrix} 7\\ 5\\ 6 \end{pmatrix} = \begin{pmatrix} |L_1|\\ |L_2|\\ |L_3| \end{pmatrix}$
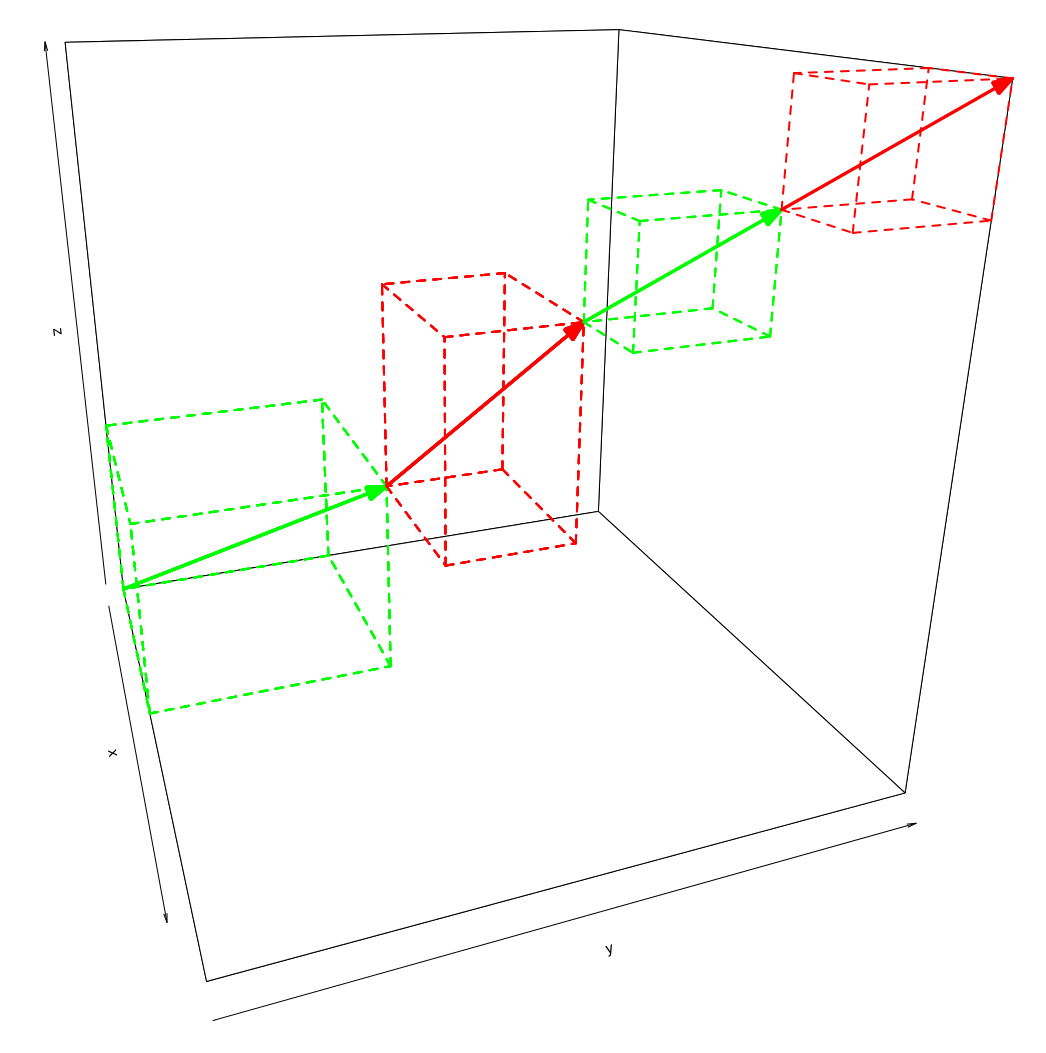
Since the position vector of alignment $n$ is given by the path of alignments $0,\ldots,n-1$ (see image), individual alignments can be expressed by the sum of preceding alignment vector in $\Delta$:
$A_n = \left(\sum_{i=1}^{n-1}{\Delta_i},\Delta_n\right)$
Part 3
* Let $\Theta(\vec{p})$ be a list of possible alignment vectors $\vec{a}_1,\ldots,\vec{a}_n$ at $\vec{p}$ with $\vec{a}\in\mathbb{N}_0^{|\mathcal{L}|} \land \vec{a}\ne \vec{0}$.
$\Theta(\vec{p})$ may contain every $\vec{x}\in\mathbb{N}_0^{|\mathcal{L}|}$ such that $\forall i (x_i \ge p_i \le |L_i|)$, but it is wise to restrict the search by a policy (for instance only allowing 3 sentences to be aligned or skipped for each language).
$A(\vec{p}_3) = \left( \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}, \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}, \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}, \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix}, \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right)$
There are no other options since $\vec{p}_3 = \begin{pmatrix} 6 \\ 4 \\ 5 \end{pmatrix}$ and $\begin{pmatrix} |L_1| \\ \vdots \\ |L_{|\mathcal{L}|}| \end{pmatrix} = \begin{pmatrix} 7 \\ 5 \\ 6 \end{pmatrix}$.
Alignment graph
See the alignment example from above as a graph:
Algorithm
Initial run
- Set run $r$ to $0$.
- Set time $t$ to $0$.
- Set position vector $\vec{p}$ to $\vec{0}$.
- Repeat until $\vec{p}_t = \begin{pmatrix} |L_1| \\ \vdots \\ |L_{|\mathcal{L}|}| \end{pmatrix}$:
- Evaluate all actions $\vec{\theta}\in \Theta(\vec{p}_t)$ with $\varphi((\vec{p}_t,\vec{\theta}),\varnothing)$ and keep the results in $\Xi$.
- For the best action $\vec{\theta}_{+}$ set $\vec{p}_{t+1}$ to $\vec{p}_t + \vec{\theta}_{+}$ and add $\vec{\theta}_{+}$ to $\Delta_r$.
- Increment $t$.
Incremental improvement
Repeated until solution is good enough (no further improvements, tbd).
- Increment $r$.
- Set time $t$ to $0$.
- Set position vector $\vec{p}$ to $\vec{0}$.
- Repeat until $\vec{p}_t = \begin{pmatrix} |L_1| \\ \vdots \\ |L_{|\mathcal{L}|}| \end{pmatrix}$:
- Evaluate all actions $\vec{\theta}\in \Theta(\vec{p}_t)$ with $\varphi((\vec{p}_t,\vec{\theta}),\varnothing)$ and keep the results in $\Xi$ unless they are already contained in $\Xi$.
- For the best action $\vec{\theta}_{+}$ set $\vec{p}_{t+1}$ to $\vec{p}_t + \vec{\theta}_{+}$ and add $\vec{\theta}_{+}$ to $\Delta_r$.
- Increment $t$.